题目大意:n*m的矩阵,从第一行走到第n行,经过的最大的格子最小是多少?
题目描述
某组织正在策划一起对某大使的刺杀行动。他们来到了使馆,准备完成此次刺杀,要进入使馆首先必须通过使馆前的防御迷阵。
迷阵由 $n\times m$ 个相同的小房间组成,每个房间与相邻四个房间之间有门可通行。在第 $n$ 行的 $m$ 个房间里有 $m$ 个机关,这些机关必须全部打开才可以进入大使馆。而第 $1$ 行的 $m$ 个房间有 $m$ 扇向外打开的门,是迷阵的入口。除了第 $1$ 行和第 $n$ 行的房间外,每个房间都被使馆的安保人员安装了激光杀伤装置,将会对进入房间的人造成一定的伤害。第 $i$ 行第 $j$ 列 造成的伤害值为 $p_{i,j}$(第 $1$ 行和第 $n$ 行的 $p$ 值全部为 $0$)。
现在某组织打算以最小伤害代价进入迷阵,打开全部机关,显然,他们可以选 择任意多的人从任意的门进入,但必须到达第 $n$ 行的每个房间。一个士兵受到的伤害值为他到达某个机关的路径上所有房间的伤害值中的最大值,整个部队受到的伤害值为所有士兵的伤害值中的最大值。现在,这个恐怖组织掌握了迷阵的情况,他们需要提前知道怎么安排士兵的行进路线可以使得整个部队的伤害值最小。
输入输出格式
输入格式
第一行有两个整数 $n,m$,表示迷阵的大小。
接下来 $n$ 行,每行 $m$ 个数,第 $i$ 行第 $j$ 列的数表示 $p_{i,j}$。
输出格式
输入输出样例
输入样例 #1
4 2
0 0
3 5
2 4
0 0
输出样例 #1
3说明
– $100\%$ 的数据,$n,m \leq 1000$,$p_{i,j} \leq 1000$。
解题思路
一共有n*m个点,深搜、广搜都会超时,但可以用堆优化,时间复杂度就是O(m*nlog(m*n)),但不可能全部点都入队,一个点至多入队4次。
程序实现
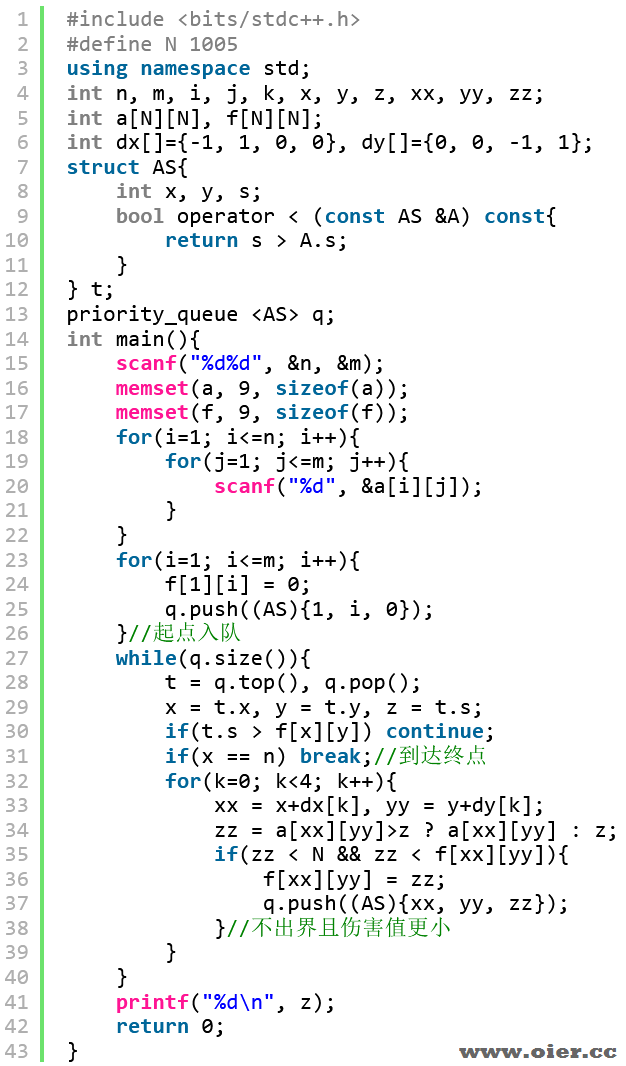
最大边最小,也是一个最小生成树问题,我们可以对边进行排序,从小到大选择,只要两个伤害值都不超过边权,合并相邻两个格子,这样就能保证合并的格子,伤害值都不超过边权,知道第一行跟第n-1行相连即可(第n行可以不读入)。

最大的最小,最小的最大,也是一个典型的二分答案问题。二分答案后,我们可以用Flood Fill验证是否连通,因为多次填充,可以用时间戳优化,避免多次memset。
