题目大意:一开始是$a^b$,两人玩游戏,每次可以让a增加1或者让b增加1,结果大于n的时候操作者就输了,请问两人都采取最优策略,最终是谁赢还是平手?
题目描述
Masha 和 Stas 正在玩一个游戏。在游戏的开始,给出一个数 $n$,同时有两个正整数 $a,b$,初始时满足 $a^b\le n$。
Masha 先手。每一回合,玩家要将 $a,b$ 的其中一个数加上 $1$,但不能使 $a^b>n$,否则该玩家输。
现在,Masha 想知道,假如两人都使用最优策略,对于同一个 $n$ 和不同的 $a,b$,谁将获胜呢?
输入输出格式
输入格式
第一行一个数 $n$。
第二行一个数 $t$,表示数据组数。
接下来 $t$ 行,每行两个数 $a,b$,描述每组数据。
输出格式
共 $t$ 行,对于每组数据:
– 若 Masha 获胜,输出 `Masha`。
– 若 Stas 获胜,输出 `Stas`。
– 若平手,输出 `Missing`。
输入输出样例
输入样例 #1
9
2
2 2
1 4 输出样例 #1
Masha
Missing说明
#### 数据规模与约定
– 对于 $30\%$ 的数据,有 $1\le n\le 2\cdot10^3$。
– 对于 $100\%$ 的数据,有 $1\le n\le 10^8$, $1\le t\le 100$, $1\le a,b,a^b\le n$。
解题思路
倒搜即可,第k次游戏时状态是$a^b$,下一次要么a加1,要么b加1,终止条件是$a^b > n$,加记忆化即不超时。
0表示我赢,1表示平手,2表示他赢。我取最小值,他取最大值。
边界条件:
1、$a^b > n$,此时轮到我,那么我赢,因为他操作后不满足条件输了,否则他赢。
2、a > 28,此时a必然是1,否则一定超过n,这个时候,大家都无法增加a,永远增加b,平手。
3、$a^2 > n$,次数b必然是1,否则一定超过n,这个时候大家无法操作b,只能操作a,谁先操作到n+1就输。
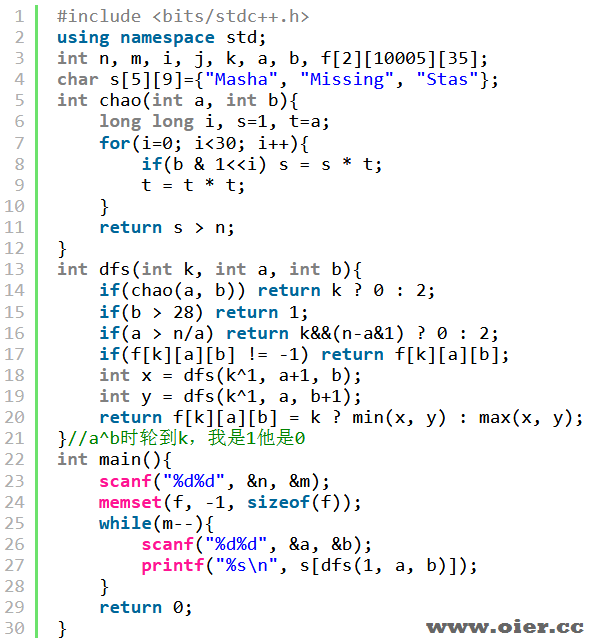
程序实现

多组询问,还可以预处理后O(1)回答。