题目大意:n个人过河,只有一条船,每次只能两个人坐船过去,耗时为最重的人的重量,n个人全部过河,至少耗时多少?
题目描述
有一个大晴天,Oliver与同学们一共N人出游,他们走到一条河的东岸边,想要过河到西岸。而东岸边有一条小船。
船太小了,一次只能乘坐两人。每个人都有一个渡河时间T,船划到对岸的时间等于船上渡河时间较长的人所用时间。
现在已知N个人的渡河时间T,Oliver想要你告诉他,他们最少要花费多少时间,才能使所有人都过河。
注意,只有船在东岸(西岸)的人才能坐上船划到对岸。
输入输出格式
输入格式
输入文件第一行为人数N,以下有N行,每行一个数。
第i+1行的数为第i个人的渡河时间。
输出格式
输入输出样例
输入样例 #1
4
6
7
10
15 输出样例 #1
42说明
[数据范围]
对于40%的数据满足N≤8。
对于100%的数据满足N≤100000。
[样例解释]
初始:东岸{1,2,3,4},西岸{}
第一次:东岸{3,4},西岸{1,2} 时间7 第二次:东岸{1,3,4},西岸{2} 时间6 第三次:东岸{1},西岸{2,3,4},时间15 第四次:东岸{1,2},西岸{3,4} 时间7 第五次:东岸{},西岸{1,2,3,4} 时间7
所以总时间为7+6+15+7+7=42,没有比这个更优的方案。
解题思路
考虑最重的人和谁过去,要么和最轻的,这样最轻的人可以把船撑回来;要么和次重的,这样可以多带更多“东西”过去。显然,如果对面有更轻的人,最重的肯定和次重的过去,否则要看哪种情况更有利。
我们考虑送最重和次重过去:
方法一:1和2过去,1回来,n和n-1过去,2回来,耗时a[1]+a[2]+a[2]+a[n]
方法二:1和n过去,1回来,1和n-1过去,1回来,耗时a[1]+a[1]+a[n-1]+a[n]
a[2]+a[2] < a[1]+a[n-1]时,先送两个小的过去,否则用最轻的送最重的过去。
程序实现
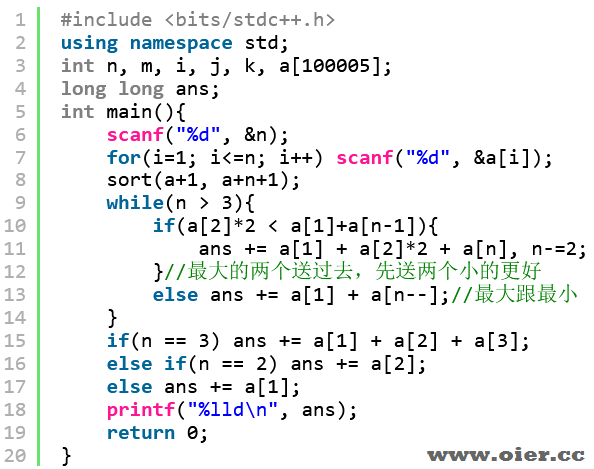
倒搜,n个人过河,c表示对面是否有第二轻的人(之前是否有两个最小的过河)。如果有,显然最重的两人过河,否则两种情况都试一下。
