洛谷P1807最长路[NOI导刊]
1890+
作者:crxis 发布:2021-05-19 分类:拓扑排序
题目大意:一个n个点m条边的有向无环图,请问从起点1到终点n,最长路径长度是多少?
题目描述
设 $G$ 为有 $n$ 个顶点的带权有向无环图,$G$ 中各顶点的编号为 $1$ 到 $n$,请设计算法,计算图 $G$ 中 $<1,n>$ 间的最长路径。
输入输出格式
输入格式
输入的第一行有两个整数,分别代表图的点数 $n$ 和边数 $m$。
第 $2$ 到第 $(m + 1)$ 行,每行 $3$ 个整数 $u, v, w$,代表存在一条从 $u$ 到 $v$ 边权为 $w$ 的边。
输出格式
输出一行一个整数,代表 $1$ 到 $n$ 的最长路。
若 $1$ 与 $n$ 不联通,请输出 $-1$。
输入输出样例
输入样例 #1
2 1
1 2 1输出样例 #1
1说明
– 对于 $20\%$的数据,$n \leq 100$,$m \leq 10^3$。
– 对于 $40\%$ 的数据,$n \leq 10^3$,$m \leq 10^{4}$。
– 对于 $100\%$ 的数据,$1 \leq n \leq 1500$,$1 \leq m \leq 5 \times 10^4$,$1 \leq u, v \leq n$,$-10^5 \leq w \leq 10^5$。
解题思路
因为五环,所以暴力广搜求最长路即可。但对于有向无环图,我们还可以用拓扑排序、深搜记忆化等方法去做,时间复杂度O(m+n)。
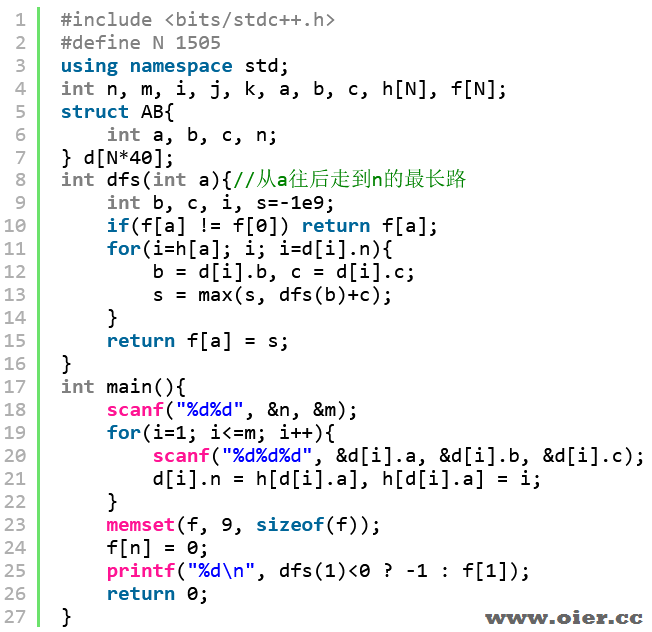
程序实现
广搜:

倒搜: