洛谷P1806跑步[NOI导刊]
3187+
作者:crxis 发布:2021-05-10 分类:递推
题目大意:将n进行自然数拆分,要求每个位置数字不一样,共有多少种方案?
题目描述
路人甲准备跑 $n$ 圈来锻炼自己的身体,他准备分多次($\gt1$)跑完,每次都跑正整数圈,然后休息下再继续跑。
为了有效地提高自己的体能,他决定每次跑的圈数都必须比上次跑的多。
可以假设他刚开始跑了 $0$ 圈,那么请问他可以有多少种跑完这 $n$ 圈的方案?
输入输出格式
输入格式
一行一个整数,代表 $n$。
输出格式
一个整数表示跑完这 $n$ 圈的方案数。
输入输出样例
输入样例 #1
212输出样例 #1
995645335说明
对于 $100\%$ 的数据,保证 $5\le n\le 500$。
解题思路
暴力记忆化:若干个格子,上一个格子填的是p-1,还剩下s没拆分,那么这个格子填p~s,填完得到1种方案,记忆化可通过。
递推方案:f[i][j]表示跑i圈,最后一次为j圈的方案数,那么之前的状态是跑了i-j圈,最后一次可以是1~j-1圈,当然也必须不超过i-j。
程序实现
爆搜,时间复杂度$O(n^3)$
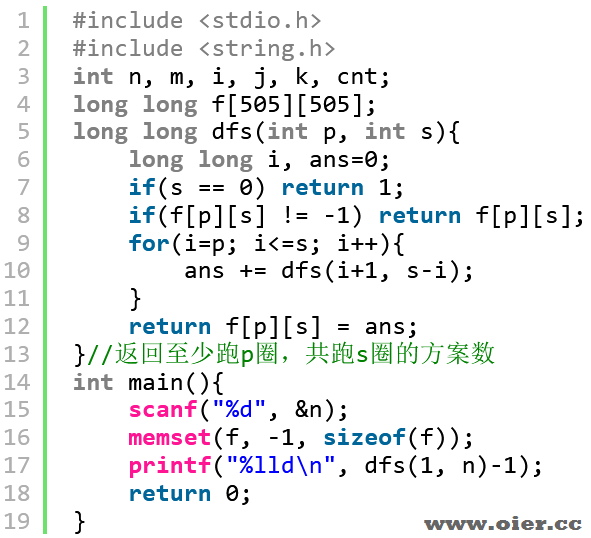
递推,不判断k是否超过i-j也行,因为默认为0,时间复杂度$O(n^3)$

前缀和优化:s[i][j]表示跑i圈,最后一圈不超过j的方案数。

降维优化,依次算出跑n圈,最后一圈是1、2、3、……n的方案数,累计起来。
