洛谷P1760通天之汉诺塔
5034+
作者：crxis 发布：2017-06-23 分类：递推
题目大意：汉诺塔由n个大小不同的圆盘和三根木柱a、b、c组成，大的圆盘不能放在小的圆盘上面，一开始全部圆盘都在a木柱，请问需要移动多少次才能把圆盘全部放到c木柱？
题目背景
直达通天路·小A历险记第四篇
题目描述
在你的帮助下，小A成功收集到了宝贵的数据，他终于来到了传说中连接通天路的通天山。但是这距离通天路仍然有一段距离，但是小A突然发现他没有地图！！！但是幸运的是，他在山脚下发现了一个宝箱。根据经验判断（小A有经验吗？），地图应该就在其中！在宝箱上，有三根柱子以及在一根柱子上的n个圆盘。小A在经过很长时间判断后，觉得这就是hanoi塔！（这都要琢磨）。但是移动是需要时间的，所以小A必须要通过制造延寿药水来完成这项任务。现在，他请你告诉他需要多少步完成，以便他造足够的验收药水。时限1s。
输入输出格式
输入格式：
一个数n，表示有n个圆盘
输出格式：
一个数s，表示需要s步。
输入输出样例
输入样例#1：
input1:31 inout2:15
输出样例#1：
output1:2147483647 output2:32767
说明
对于所有数据n<=15000
很容易的练手题哦！
解题思路
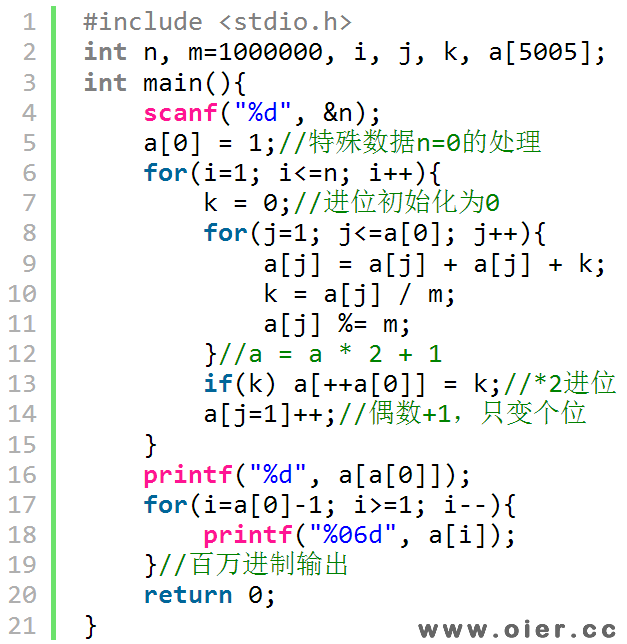
设hn为n个圆盘从a移动到c上所需要移动的次数。当n=1时，需要移动一次；当n=2时，需要先把小的盘移到b，把大的盘移到c，再把小的盘移到c，需要移动3次；以此类推，当n>=2时，需要借助c把a中的n-1个盘移动到b（hn-1次，因为a到b跟a到c是等价的），再把最大的盘移动到c（1次），最后借助a把b中的n-1个盘移到c（hn-1次），即hn = hn-1 * 2 + 1
简单优化：不难发现，hn = hn-1 * 2 + 1，也即hn = 2n – 1，用这个公式好像可以少加很多次1？？？
更多优化：复杂度是O(n*位数)，如果降低位数？可以使用万进制、百万进制，还可以使用十亿进制，因为十亿*2+1还是在int范围内！
程序实现
