题目大意:n个数,m个询问,每次询问区间选出两个数是相同的概率,输出最简分数。
题目描述
upd on 2020.6.10 :更新了时限。
作为一个生活散漫的人,小 Z 每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天,小 Z 再也无法忍受这恼人的找袜子过程,于是他决定听天由命……
具体来说,小 Z 把这 $N$ 只袜子从 $1$ 到 $N$ 编号,然后从编号 $L$ 到 $R$ ($L$ 尽管小 Z 并不在意两只袜子是不是完整的一双,甚至不在意两只袜子是否一左一右,他却很在意袜子的颜色,毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小 Z,他有多大的概率抽到两只颜色相同的袜子。当然,小 Z 希望这个概率尽量高,所以他可能会询问多个 $(L,R)$ 以方便自己选择。
**然而数据中有 $L=R$ 的情况,请特判这种情况,输出`0/1`。**
输入输出格式
输入格式
输出格式
输入输出样例
输入样例 #1
6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6输出样例 #1
2/5
0/1
1/1
4/15说明
$30\%$ 的数据中,$N,M\leq 5000$;
$60\%$ 的数据中,$N,M \leq 25000$;
$100\%$ 的数据中,$N,M \leq 50000$,$1 \leq L < R \leq N$,$C_i \leq N$。
解题思路
概率即合法方案除以总方案,区间长度为y,那么总方案是$C_y^2$;合法方案为每种数字的方案数量之和。对于单种数字原来有x个,如果多了一个,那么方案数由$C_x^2$变为$C_{x+1}^2$,增加的数量为$C_{x+1}^2 – C_x^2 = x$。减少一个同理。
由于时限200ms,怕超时,可以加入奇偶排序优化:奇数块右端点递增,最后一个区间右端点会比较靠右;偶数块右端点递减,这样右端指针不需要一下子往回走到左端点,可能会快一些。
莫队的时间复杂度是$O(m\sqrt{n} + n\sqrt{n})$,因为每个询问(m个),左端点移动的范围是根号的,而且每一块(根号块),右端点移动的总和是O(n)的。
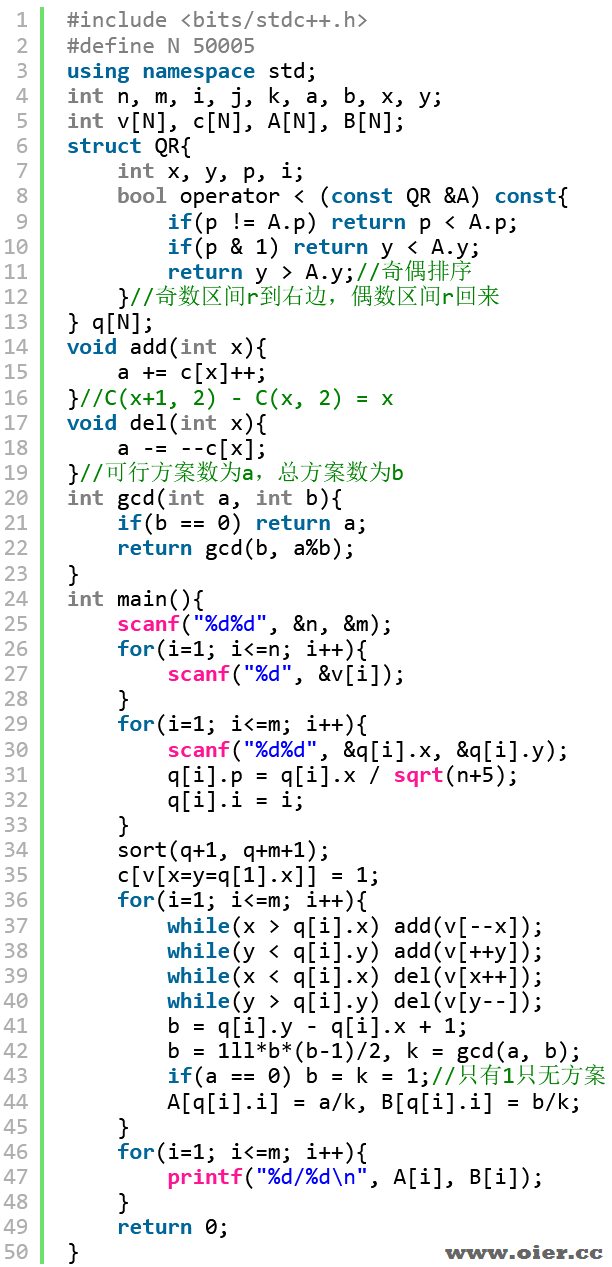
程序实现