洛谷P1341无序字母对
4201+
作者:crxis 发布:2017-10-19 分类:欧拉回路
题目大意:给定n个各不相同的无序字母对,请构造一个有n+1个字母的字符串使得每个字母对都在这个字符串中出现。
题目描述
给定n个各不相同的无序字母对(区分大小写,无序即字母对中的两个字母可以位置颠倒)。请构造一个有n+1个字母的字符串使得每个字母对都在这个字符串中出现。
输入输出格式
输入格式:
第一行输入一个正整数n。
以下n行每行两个字母,表示这两个字母需要相邻。
输出格式:
输出满足要求的字符串。
如果没有满足要求的字符串,请输出“No Solution”。
如果有多种方案,请输出前面的字母的ASCII编码尽可能小的(字典序最小)的方案
输入输出样例
输入样例#1:
4 aZ tZ Xt aX
输出样例#1:
XaZtX
说明
【数据规模与约定】
不同的无序字母对个数有限,n的规模可以通过计算得到。
解题思路
首先,n是多少呢?两个字母组成的字符串,第一个字母可从52个中选一个,第二个字母可从剩下51个里选哪一个,去掉重复即52*51/2那么多个,不超过1500。
其次,要求每个字母对都要出现且只出现一次。把字母对看成是边,字母看成是点,那么每条边都要走一次,即欧拉回路。建图后统计奇点个数,不是0也不是2就无解,有解的话用深搜寻找欧拉(回)路,如果找完路之后,路径长度刚好是n+1则每条边都走了一次,否则建的图是非连通图,无解。找到路径后,倒着输出即是答案。
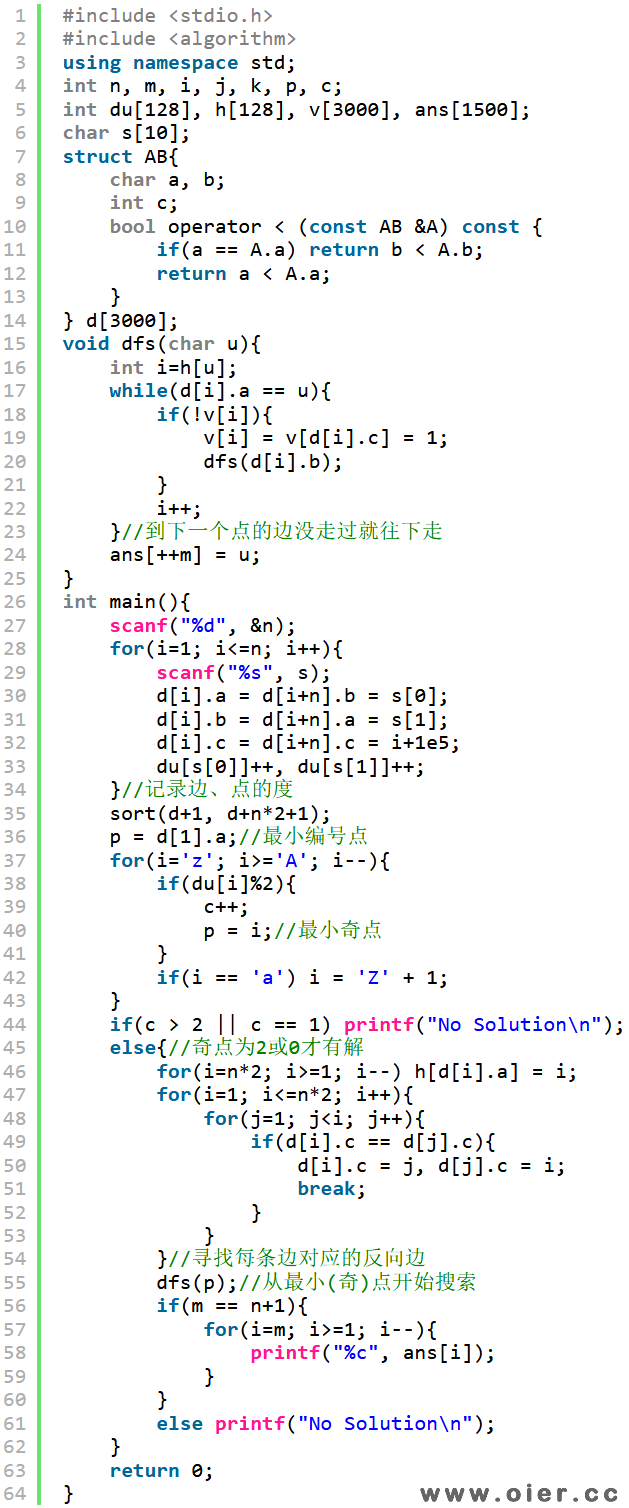
程序实现