题目大意：一项工程有n个子任务，任务之间在时间上有先后关系，什么时间该开始什么任务呢？

题目描述

造一幢大楼是一项艰巨的工程，它是由n个子任务构成的，给它们分别编号1，2，…，n(5≤n≤1000)。由于对一些任务的起始条件有着严格的限制，所以每个任务的起始时间T1，T2，…，Tn并不是很容易确定的(但这些起始时间都是非负整数，因为它们必须在整个工程开始后启动)。例如：挖掘完成后，紧接着就要打地基；但是混凝土浇筑完成后，却要等待一段时间再去掉模板。

这种要求就可以用M(5≤m≤5000)个不等式表示，不等式形如Ti-Tj≤b代表i和j的起始时间必须满足的条件。每个不等式的右边都是一个常数b，这些常数可能不相同，但是它们都在区间(-100，100)内。

你的任务就是写一个程序，给定像上面那样的不等式，找出一种可能的起始时间序列T1，T2，…，Tn，或者判断问题无解。对于有解的情况，要使最早进行的那个任务和整个工程的起始时间相同，也就是说，T1，T2，…，Tn中至少有一个为0。

输入输出格式

输入格式：

第一行是用空格隔开的两个正整数n和m，下面的m行每行有三个用空格隔开的整数i，j，b对应着不等式Ti-Tj≤b。

输出格式：

如果有可行的方案，那么输出N行，每行都有一个非负整数且至少有一个为0，按顺序表示每个任务的起始时间。如果没有可行的方案，就输出信息“NO SOLUTION”。

输入输出样例

5 8
1 2 0
1 5 –1
2 5 1
3 1 5
4 1 4
4 3 –1
5 3 –1
5 4 –3

0
2
5
4
1

5 5
1 2 –3
1 5 –1
2 5 –1
5 1 –5
4 1 4

NO SOLUTION

解题思路

两个未知数的差小于等于某个常数（大于等于也可以，因为左右乘以-1就可以化成小于等于），这样的不等式组就称作差分约束系统，差分约束可以转化成求最短路径。

如Ti-Tj≤b，即Ti≤Tj+b，与求最短路很相似，建立j到i的一条有向边，权值为b，这样，到i的距离越短越不会出问题。对于所有的约束关系，都建立一条有向边，然后求最短路径，求完后，必定满足所有约束条件（如果不满足，会继续进行松弛操作，从而更新Ti的最短路径，使得Ti≤Tj+b）；如果求不完，即出现负环，那么输出“NO SOLUTION”。

如何判断负环呢？如果用SPFA求最短路径，那么一个点重复入队超过n次就说明出现负环（松弛次数）；如果用深搜求最短路径，那么一路搜下去，搜回自己或者搜到访问过的点，就是出现负环。

首先介绍一下SPFA的做法：首先是建图，把差分约束系统中的所有不等式都转换成图中的边（边权可以是负数），然后求单源最短路径。这个单源是谁呢？我们可以建立一个源点0（如果0被用了，可以用n+1、n+2等编号），然后从源点向其他各点连一条权值为0的有向边（Ti<=T0+0），代表其他子任务可以同时开始做，然后从源点跑一遍SPFA求单源最短路径，最后可能出现负数时间，让所有时间都减去最小的那个时间，就能让最小的时间从0开始了。求完后，发现这个超级源点也没什么用，实际上他根问题本身没有任何关系，至少让各个任务编号可以入队而已，因此，我们也可以手动把所有子任务的点入队，直接进行松弛操作，二不要这个超级源点。

接着介绍一下判断负环的方法：如果出现负环，一个点需要重复入队n次，就好像跑了n次的SPFA一样，时间复杂度是O(kmn)，如果n和m都超过10000，那么很容易超时的！还有一种方案就是深搜判断负环，不用SPFA也不用队列了，直接依次搜索n个点，循环这n个点到其他各个点的最短路径，如果在寻找最短路径的过程中，搜到了搜过的点，说明出现负环。这两种方法，在判断负环上，深搜可能更快出结果。因此，对于n*m小于5000万的话，SPFA还是可以接受的，否则有可能超时，选深搜可能更好。

最后讲一下SPFA队列的大小：如果不出现负环，入队的点数一般不超过边数的10倍，一旦出现负环，入队的点数就是非常多的。因此，我们不能直接开一个大数组。我们可以用STL里面的队列，或者自己写一个循环队列。当然，你自认为运气好的话，可以直接开50倍边的队列，当入队次数超过50倍边，直接判断他出现负环。

程序实现

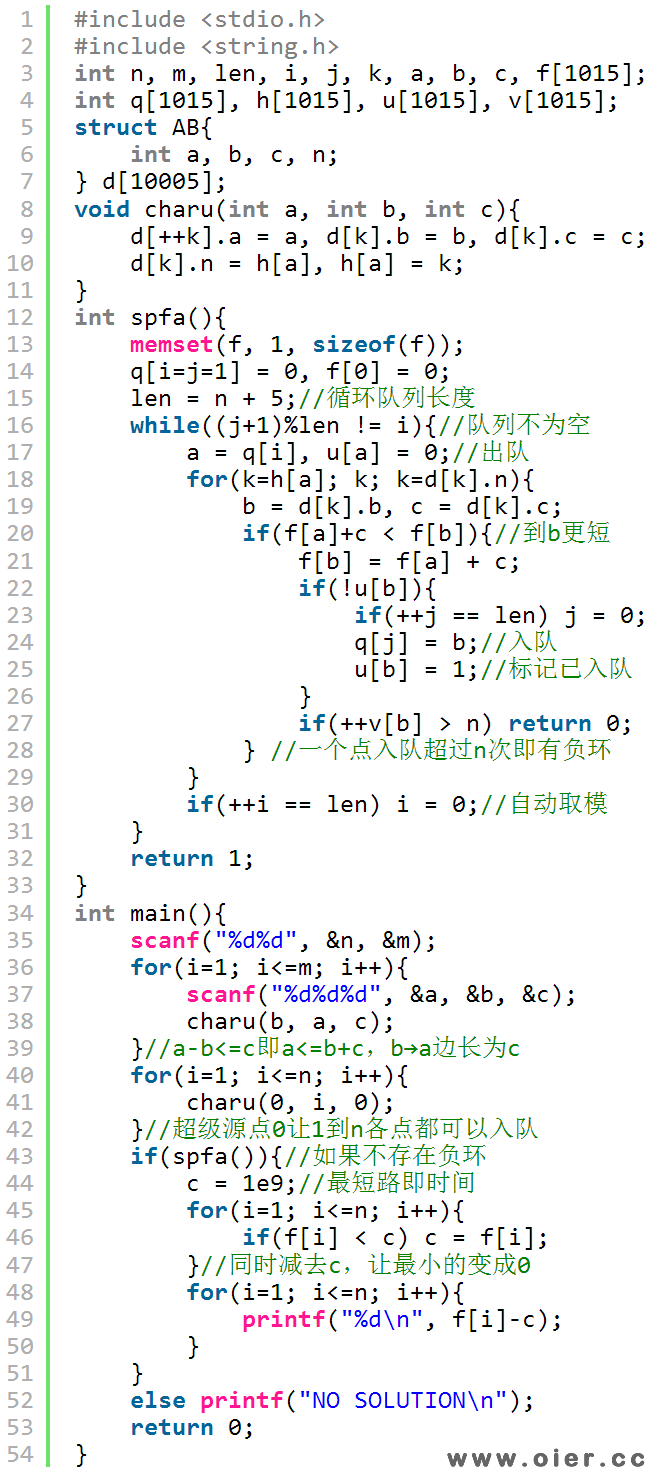
1、循环队列

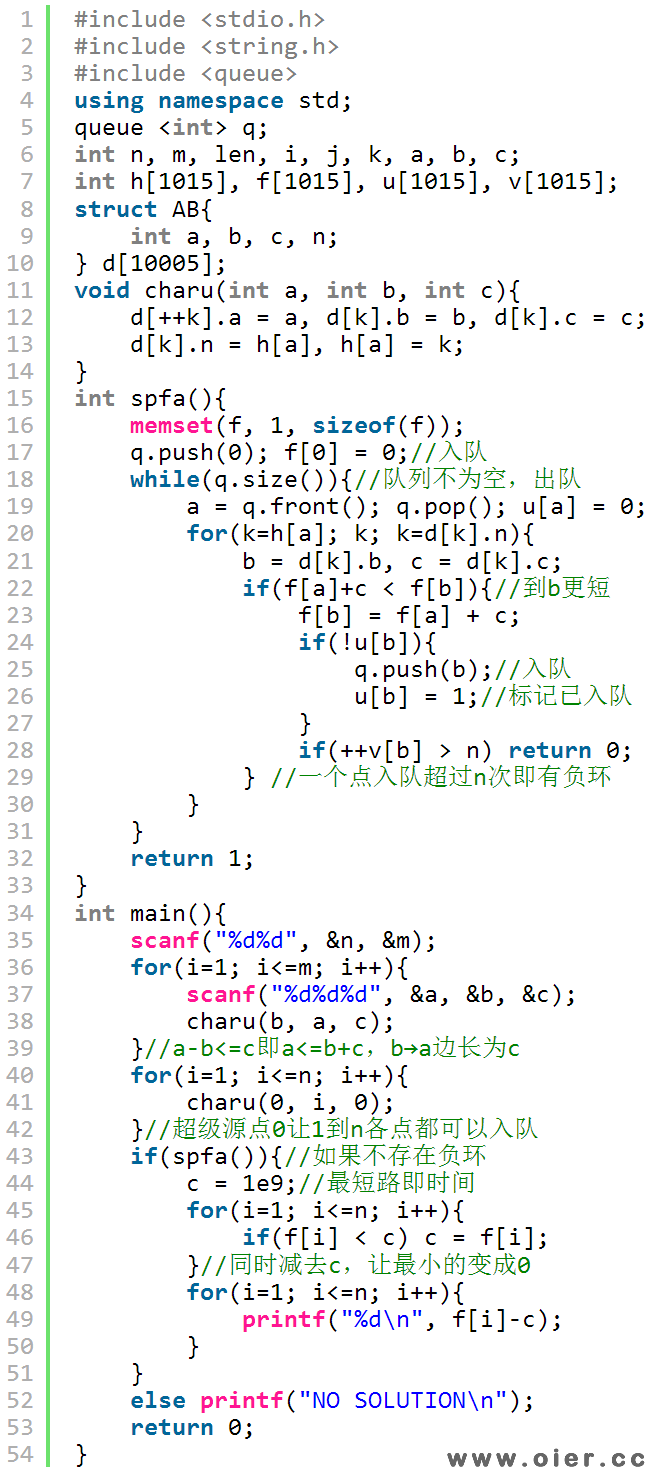
2、使用STL队列

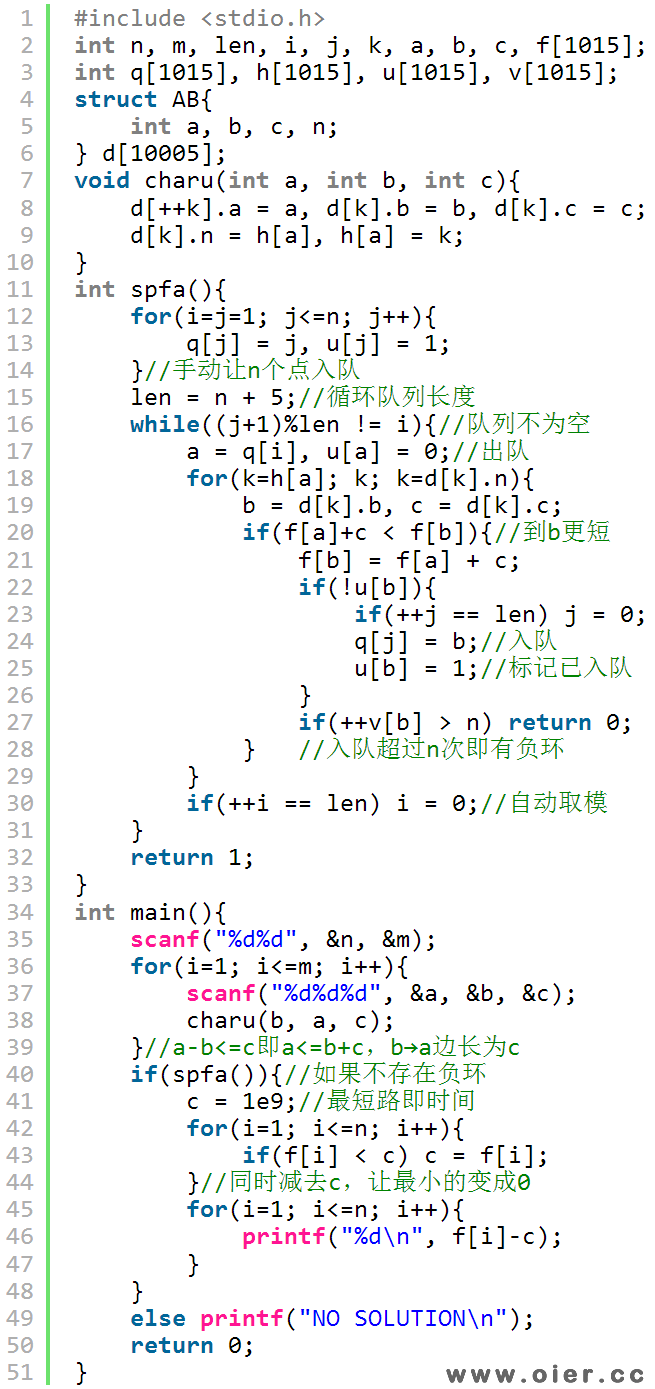
3、手动入队

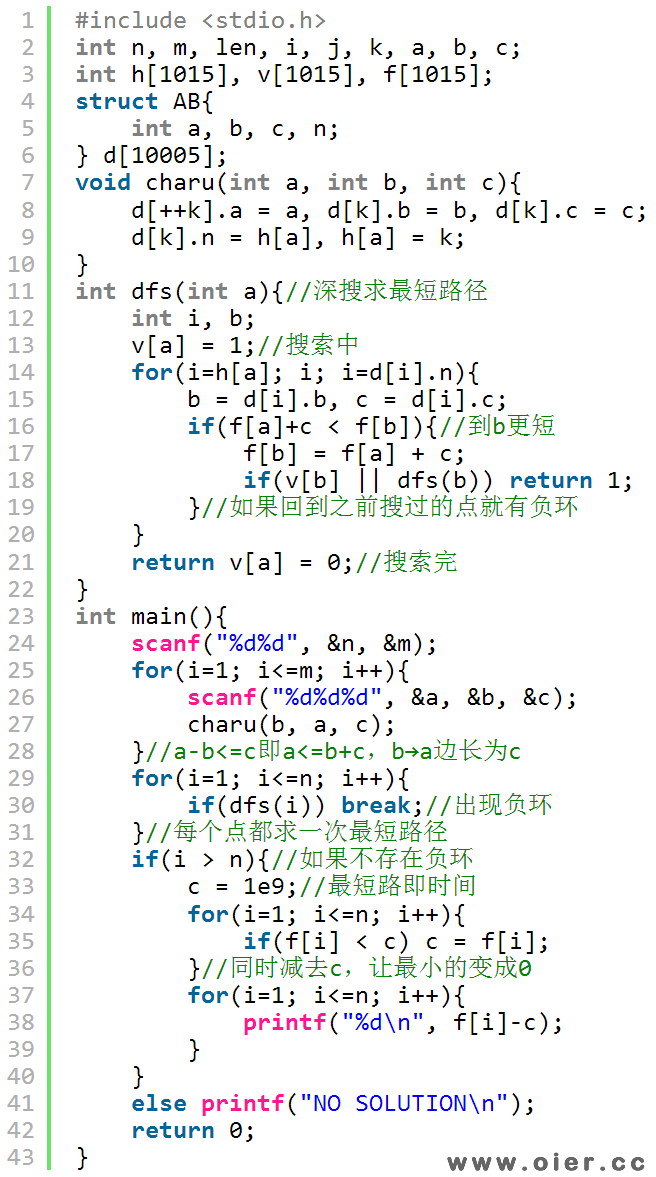
4、深搜求最短路径

5、SPFA队列长度一般是边数量的10倍，超过太多的话，极有可能出现负环，但也有可能没有负环。