洛谷P1250种树
2458+
作者：crxis 发布：2017-12-30 分类：差分约束
题目大意：有n块地，每块地至多种一棵树，m个居民分别认为某一段地至少种x棵树，请问至少种多少棵树？
题目描述
一条街的一边有几座房子。因为环保原因居民想要在路边种些树。路边的地区被分割成块，并被编号成1..N。每个部分为一个单位尺寸大小并最多可种一棵树。每个居民想在门前种些树并指定了三个号码B，E，T。这三个数表示该居民想在B和E之间最少种T棵树。当然，B≤E，居民必须记住在指定区不能种多于区域地块数的树，所以T≤E-B+l。居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。
写一个程序完成以下工作：
输入输出格式
输入格式：
第一行包含数据N，区域的个数(0<N≤30000)；
第二行包含H，房子的数目(0<H≤5000)；
下面的H行描述居民们的需要：B E T，0<B≤E≤30000，T≤E-B+1。
输出格式：
输出文件只有一行写有树的数目
输入输出样例
输入样例#1：
9 4 1 4 2 4 6 2 8 9 2 3 5 2
输出样例#1：
5
解题思路
f数组记录前缀和，f[i]表示前面i块地种树数量，那么[a,b]至少种c棵树，即f[b] >= f[a-1] + c。此外，每块地只能种一棵树，那么f[i]比f[i-1]至多多1，即f[i] – f[i-1] <= 1，转成>=就是f[i-1] >= f[i] – 1。还有就是不能种负树，后面的一定比前面多，即f[i] >= f[i-1]。全部转成大于等于后，求最长路即可，求出的最长路，就是刚好满足条件的最小值。
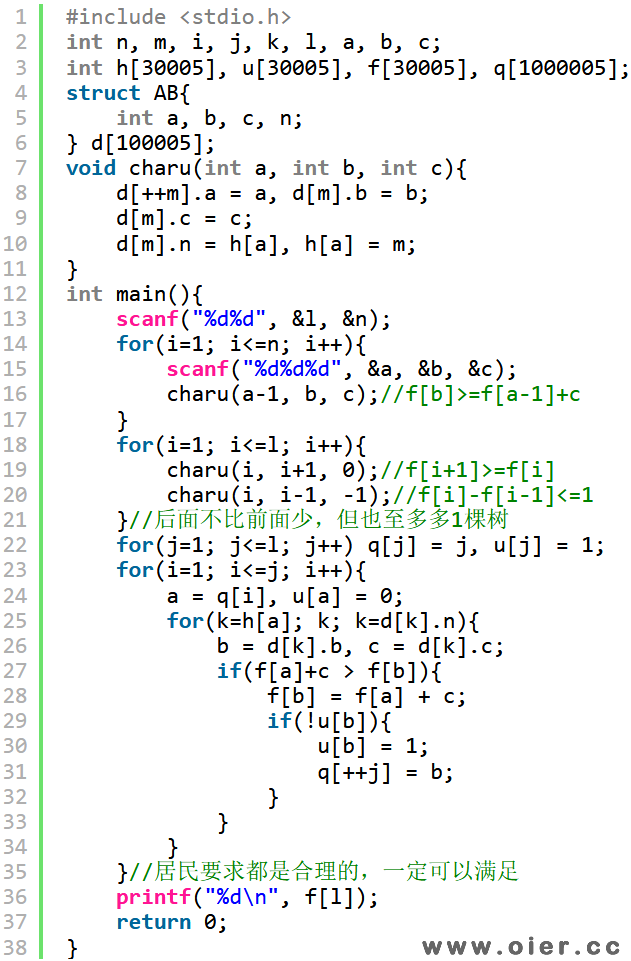
程序实现
