题目大意:在一个有向完全图中,从第一个点出发的哈密顿回路最短是多少?
题目描述
某乡有n个村庄(),有一个售货员,他要到各个村庄去售货,各村庄之间的路程s(0<s<1000)是已知的,且A村到B村与B村到A村的路大多不同。为了提高效率,他从商店出发到每个村庄一次,然后返回商店所在的村,假设商店所在的村庄为1,他不知道选择什么样的路线才能使所走的路程最短。请你帮他选择一条最短的路。
输入输出格式
输入格式:
村庄数n和各村之间的路程(均是整数)。
输出格式:
最短的路程。
输入输出样例
3 0 2 1 1 0 2 2 1 0
3
说明
输入解释
3 {村庄数}
0 2 1 {村庄1到各村的路程}
1 0 2 {村庄2到各村的路程}
2 1 0 {村庄3到各村的路程}
解题思路
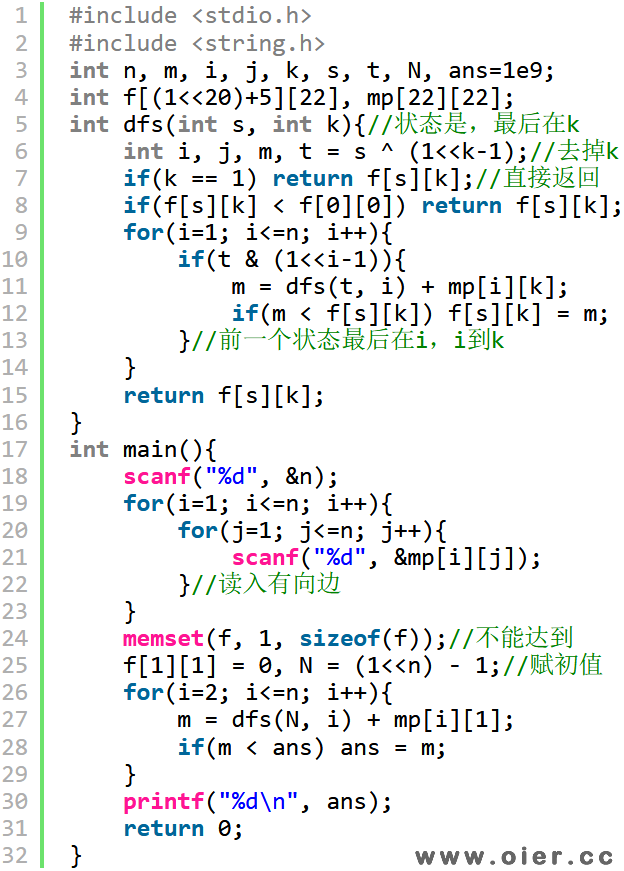
这是TSP问题(Travelling Salesman Problem),又名旅行推销员问题、货郎担问题,是数学领域中著名的问题之一。这里介绍一下状态压缩的动态规划解法。
首先是状态,f[i][j]表示状态是i,最后到达的是第j个村庄的最短距离。如i=13(1101)、j=3,那么表示推销员已经到过村庄1、3和4,且最后到达的村庄是3。
其次是顺序,用已知的状态推出未知的状态。所谓已知,即已经是最短距离的状态,后面不会再更新到他的。那么状态递推的顺序就是从小到大,从1到(1<<n)-1。如枚举状态i=13时,二进制下1101去掉1个1的状态已经不会到出现了,也就是说该状态不会再被更新,是已知的、不变的。
然后推出下一个状态,当前状态是13,那么可以到达哪些状态呢?从最后的村庄再走一步到下一个没到过村庄,就会多一个1,多到一个村庄了,这就需要枚举最后的村庄和没到过的村庄。最后更新状态最短距离。
优化与剪枝:第一个村庄是必到的,且不会出现没到过第一个村庄的情况,因此,枚举的状态都是奇数,从1开始枚举,每次加2可以快一倍;如果f[i][j]状态到过,那么不等于初值f[0][0],到过才考虑从j走向下一个村庄;下一个村庄枚举从2到n,因为最后才回到1,判断是否没到过,只需要看状态i里面是否村庄对应的1。
位运算技巧:判断状态i第k位是否有1,可以用i&(1<<k-1);多到第k个村庄,可以用i|(1<<k-1);减号优先于位运算符,之所以要建议,因为1本身在第一位。
程序实现

暴力搜索哈密顿回路,用距离等进行剪枝,80分:读入边后,从起点a开始搜索,走到a的距离是s,走过了c个村庄,如果c==n,那么走完了,记录最小距离(需要走回1);否则,继续找下一个没走过的村庄,更新参数a、s、c后继续搜索;搜索过程中,可以进行最优性剪枝,如果不比最优值ans小,后面就无法更新ans了,直接return。
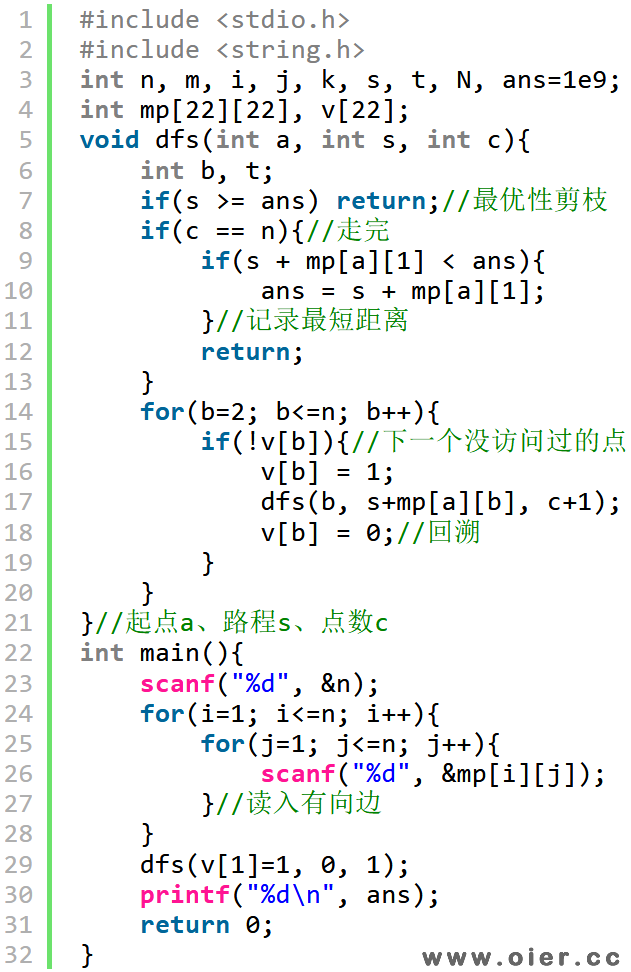
爆搜+记忆化剪枝,90分:

状态压缩的记忆化搜索,为什么还是90分?