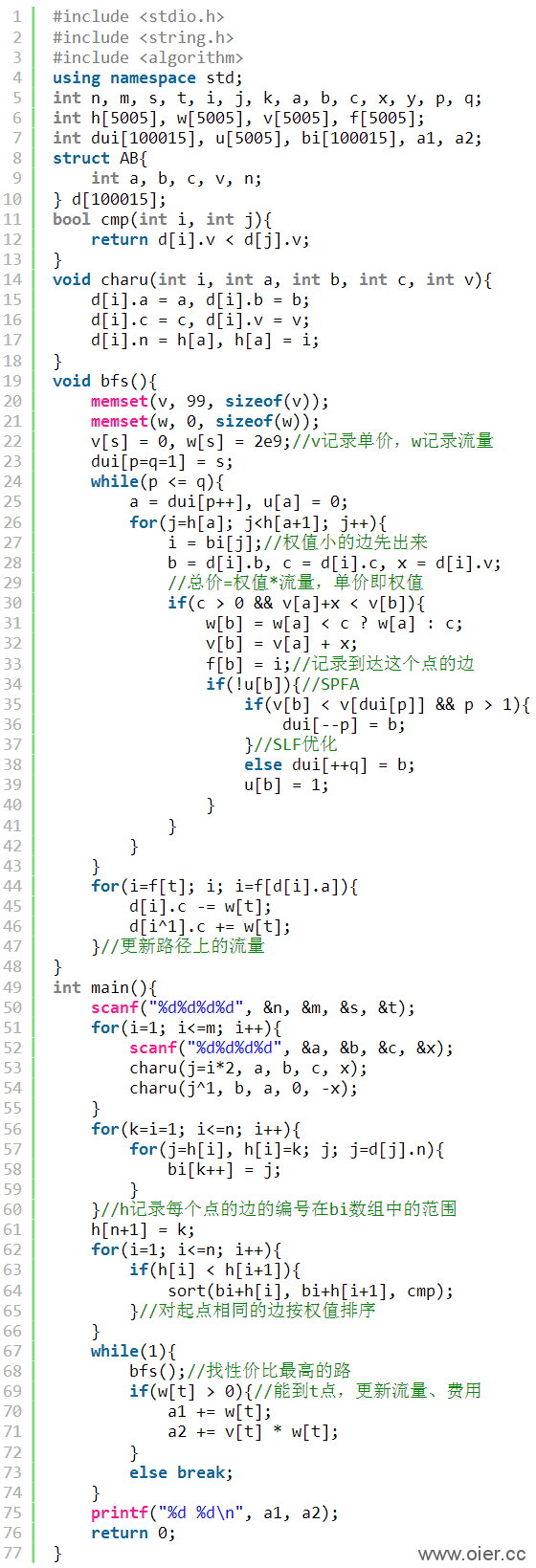
这是一道最小费用最大流的模板题,文中用的是spfa解决的,其中有两个优化:1、SLF(Small Label First)优化;2、边排序优化。
题目描述
如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含四个正整数ui、vi、wi、fi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi),单位流量的费用为fi。
输出格式:
一行,包含两个整数,依次为最大流量和在最大流量情况下的最小费用。
输入输出样例
输入样例#1:
4 5 4 3 4 2 30 2 4 3 20 3 2 3 20 1 2 1 30 9 1 3 40 5
输出样例#1:
50 280
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=5000,M<=50000
样例说明:
最优方案如下:第一条流为4–>3,流量为20,费用为3*20=60。
第二条流为4–>2–>3,流量为20,费用为(2+1)*20=60。
第三条流为4–>2–>1–>3,流量为10,费用为(2+9+5)*10=160。
故最大流量为50,在此状况下最小费用为60+60+160=280。
故输出50 280。
解题思路
在网络流图中每条边,加上运输货物的费用,求解最大流下的最小费用,即最小费用流。
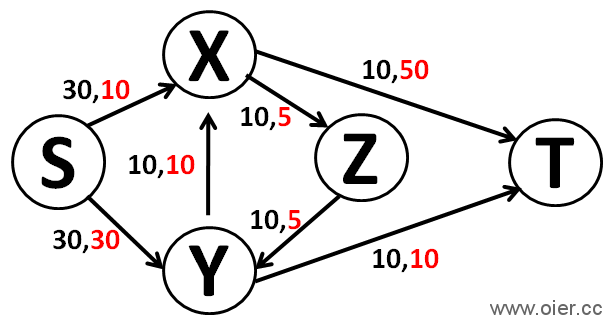
思考:如图,运输1个流量的最小费用是多少?2个呢?3个呢?……第一次从那条路运输?为什么?运输之后会出现流量大于0的负边,会造成死循环吗?是否可能出现负环(环中权值之和为负数)?
简答:30,60,90;S→X→Z→Y→T,因为这条路费用低;不会有负环,若出现负环,则之前肯定没有选费用最低的路,只要不出现负环就不会有死循环。
网络流是不断寻找从S到T的路,最小费用流只需要稍稍改动一下——不断寻找S到T单位流量费用最小的路,直到没有路为止。
如何找单位流量最小的路呢?其实把费用看成路程,最短路径就是这个最小单价了。因为无论运多少货物过去,总价=费用和*流量,单价即费用和!
因此,只需要稍微改动一下网络流的代码,就可以实现最小费用流了。
程序实现
1、基本实现:注意第17、24、28行的代码,主要是条件的变化和spfa的优化。条件不再是没访问过才搜索,而是有更小费用(更短路径)就要重新搜索。加入u数组,判断点是否在队里中,不在队列中才入队,这就是bfs和spfa的重要区别。原题时限2s,程序可以通过;即使是1s时限,通过优化输入输出、变量存储也可以通过此题。

小优化补充:上述代码第28行,条件改为(!u[b] && b!=t),可以避免终点t入队,速度会稍快一些!
2、为了追求更高的速度,需要想尽办法优化程序。SPFA中如果能到达b点且费用更低,则需要更新入队。为了降低入队的频率,我们可以尽量先搜索费用低的点。(如果每次搜索的都是费用最低的点,那还会重新入队吗?q能否控制在n以内?)为了方便程序实现,我们仅作一点点优化,即在入队的时候,如果b点单价比队头单价更低,则让b点先被搜索。只要p能减一,就可以把b放到对头(这样队列的数组也可以开小一点,但这不是重点)。这个小小的优化,时间比前一个程序至少快一倍,能轻松在1ms内通过此题。

3、上一个代码,仅仅对队头做了优化,然而队列中有很多点都没有被优化过。搜索是无序的,但我们可以人为的干预他,让他尽量有序。用邻接表存储的边是无序的,但我们却可以给他们排序,让边权小的边先搜索,这样,同一个点扩展出来的点的费用,必定单调不减,从而实现费用小的点先搜索。代码3的速度是代码2的两倍左右。
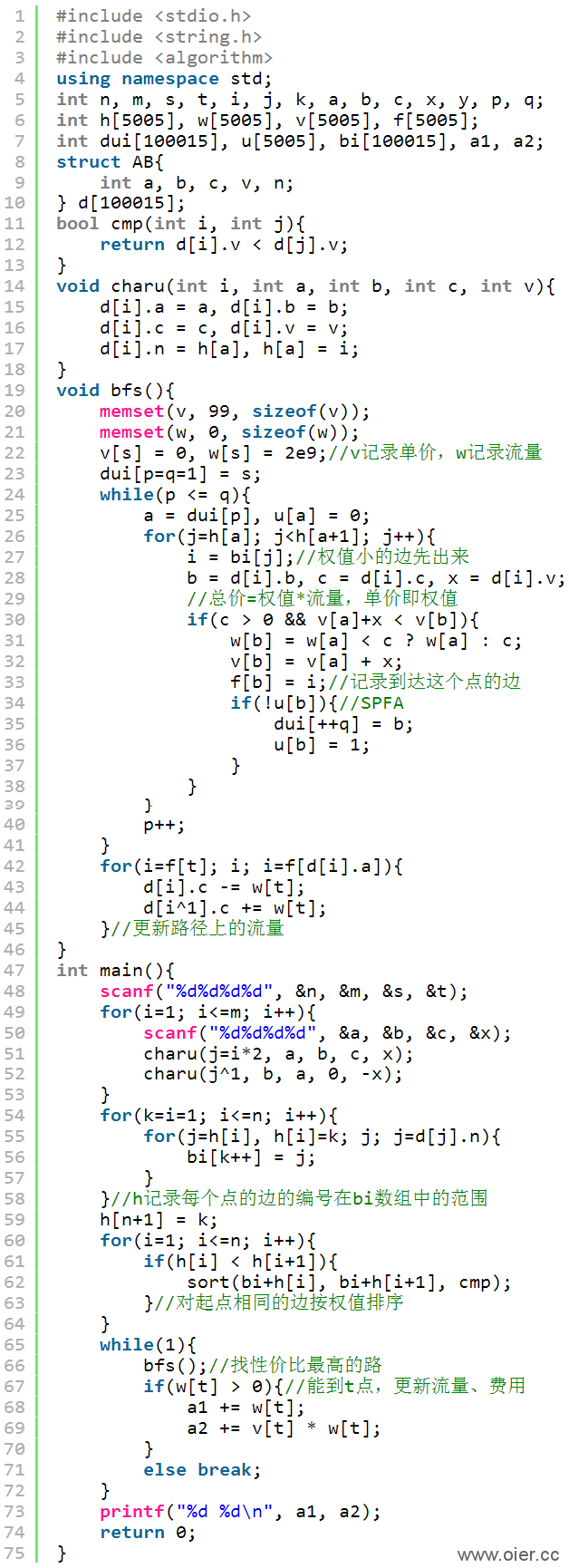
4、边排序和SLF结合在一起,比代码3快25%-35%左右。